Easy Way to Find Coupling Cap Values!
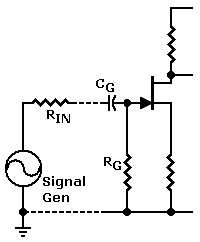
It's Accurate & It's Fast. If you can find a moment's peace, you can even run the calcs in your head! We start with the input capacitor, where we put on the thinking hat. We imaginarily connect the gate resistor RG and the “generator resistance” RIN in series. The generator resistance is the resistance of your previous stage. Or RIN could be the internal resistance of your guitar pickup.
Don't know the generator resistance? Just ignore it for now. We can adjust it later, after we try playing through the amp and see how it sounds.
|
|
|
Rule of Tens
Simplify Your Calculations. The world of coupling capacitors isn't perfect. Manufactured capacitors are only available in certain values. Plus, plain-vanilla capacitor values have tolerances, sometimes wide tolerances. These facts encourage us to build a little leeway into our designs. In fact, our coupler design method defers to the age-old Rule of Tens...
→ Rule of Tens. A value within 10 percent performs well in most circuits. A calculation within 10 percent is usually accurate enough.When you figure capacitor values, you depend on impedances and resistors in ohms. Your calculations will go easier if you use round values within 10 percent. The result will remain satisfactory. For example, if you need to know the parallel resistance of a 10K and and 1K resistor, you may skip the calculation! Instead, just use the 1K value. The 1K is close enough to the 909-ohm value that your calculation would crank out.
Output Coupling Capacitor
Capacitor Leakage
♦ CAUTION. Electrolytic capacitors, even new ones, leak current. A FET can detect and amplify this leakage. In some high-impedance circuits (including even regular transistor circuits), an electrolytic capacitor can upset the bias of the input stage. The symptom of this is that the input will load down. Loading affects the achievable swing of the stage. In severe cases, the device will latch to one of the power rails.
The only solution is to swap out the coupling capacitor for a higher quality capacitor. You can expect that the replacement part won't be electrolytic. Just to be sure that you don't have a bad part, try another part of the same type and value. If the symptom persists, use a polyester, polystyrene, teflon or Mylar capacitor. This new choice might force you to increase the lowest input frequency, or change to a new design.